
학습내용
#1 : 지수함수(expotential function)
지수함수는 지수에 미지수 x가 있는 함수로 인공지능의 오차역전파에 사용하는 수학.
- f(x) = ax(a > 0, a ≠ 1) 형태로 나타낼 수 있는 함수.
- 밑은 양의 정수어야 하며 a의 범위는 a > 0, 0 < a <1이다.
파이썬에서의 지수 함수
파이썬에서는 math 라이브러리의 pow(), sqrt(), exp()함수를 사용해 지수 함수를 쓸 수 있다.
import math
#x의 y 제곱
pow = math.pow(2, 4)
print(pow)
#16.0
#x의 제곱근
sqrt = math.sqrt(4)
print(sqrt)
#2
#e(자연상수)의 x제곱
exp = math.exp(2)
print(exp)
#7.38905609893065
#e(자연상수) 값
sqrt2 = math.sqrt(exp)
print(sqrt2)
#2.718281828459045- math.pow(x, y) : x의 y제곱.
- math.sqrt(x) : x의 제곱근.
- math.exp(x) : e(자연상수, 2.718281828459045)의 x제곱.
#2 : 지수함수 그래프(expotential function graph)
지수함수에서 지수가 커지면 y 값도 커지고, 지수가 작아지면 y값도 작아진다.(y>0) 따라서, 지수 x가 커지면 y도 커지고 그 지수의 값이 커질 수록 y값의 증가도 커지기에 오른쪽 위로 휜 그래프가 된다.
| a가 2일 때 (a>0) | |||||||
| x | ··· | -2 | -1 | - | 1 | 2 | ··· |
| y=ax | ··· | 1/4 | 1/2 | 1 | 2 | 4 | ··· |
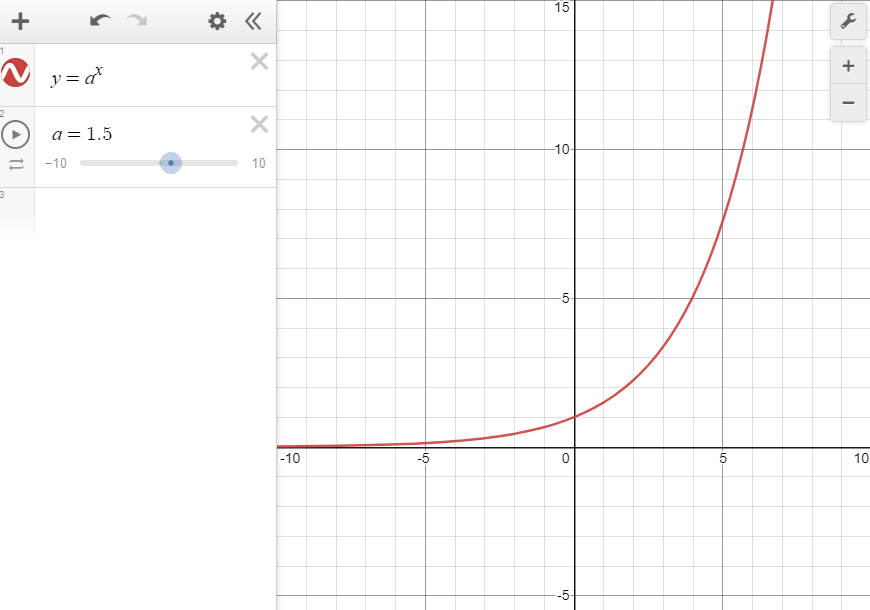
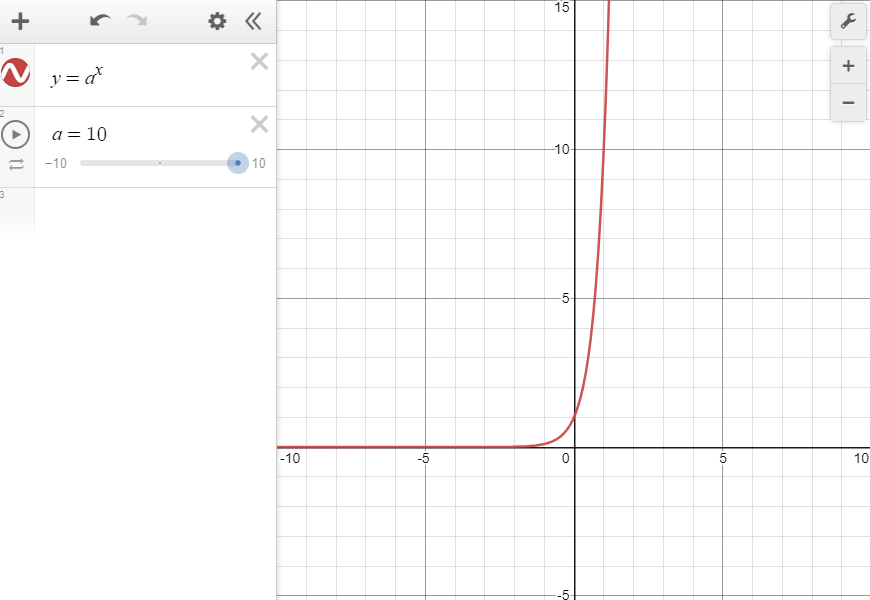
반대로, 지수 y가 작아지면 y도 작아지기 때문에 0에 한 없이 가까워지는 오른쪽 아래로 휜 그래프가 된다.
| a가 1/2일 때 (0<a<1) | |||||||
| x | ··· | -2 | -1 | 0 | 1 | 2 | ··· |
| y=ax | ··· | 4 | 2 | 1 | 1/2 | 1/4 | ··· |


이때 밑이 역수인 두 지수함수는 y축에 대해 대칭이다. 2와 1/2, 8과 1/8 등.


#3 : 지수함수의 평행 이동과 대칭 이동
지수함수의 평행 이동(parallel translation)
평행 이동은 그래프 모양은 유지하고 위치만 바꾸는 것.
- f(x, y) = 0을 (p, q)만큼 이동한다면 f(x - p, y - q) = 0이 된다.


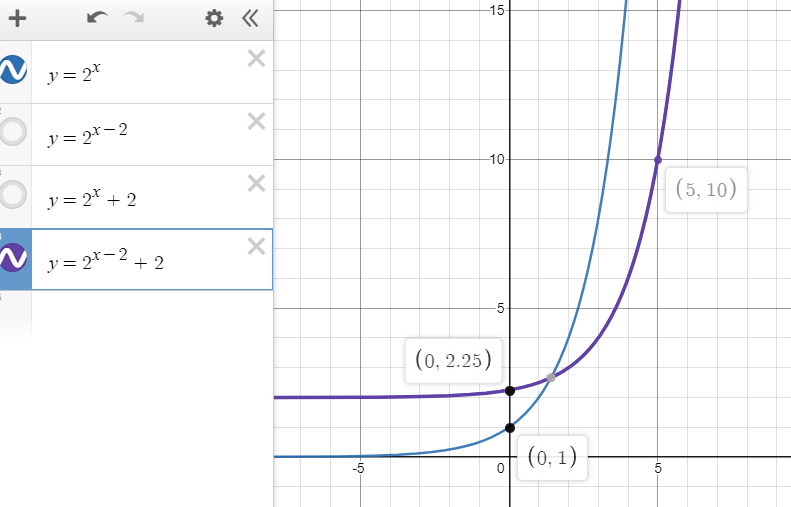
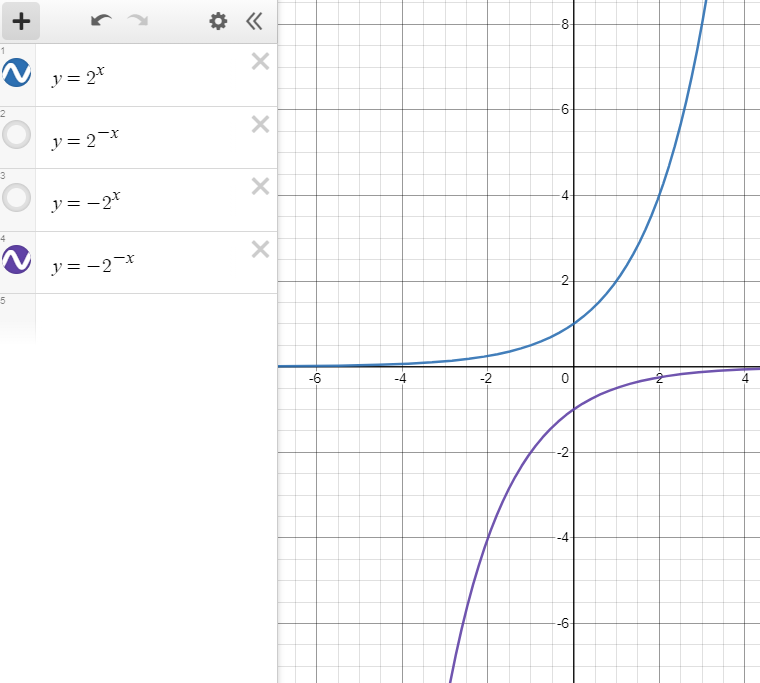
지수함수의 대칭 이동(symmetric transposition)
x축, y축, 원점을 기준으로 대칭이동을 할 수 있다.
- y=ax 그래프를 대칭이동 한다면.
- x축 대칭이동 : (-y=ax) = (y=-ax)
- y축 대칭이동 : y=a-x
- 원점 대칭이동 : (-y=a-x) = (y=-a-x)


'수학 > 기초수학' 카테고리의 다른 글
| [기초 수학] 5. 로그함수(log function) (0) | 2021.10.05 |
|---|---|
| [기초 수학] 3. 기울기, 제곱근, 인수분해 (0) | 2021.10.03 |
| [기초 수학] 2. 함수, 일차함수, 이차함수, 그래프 (0) | 2021.09.28 |
| [기초 수학] 1. 방정식과 부등식 (0) | 2021.09.28 |
| [예대생의 수학] 나는 왜 수학을 공부하려고 하는가 (0) | 2021.09.27 |




댓글